maths are hard and i've no clue how they are useful in life
basic skills is the other story, still can't figure our why limits and integral garbage are so important
im not going through that ever again
chain and product rule probably is very important for u to learn,
integral(e^-x) is -e^-x
only way to solve this is by what triple said, F(b) - F(a) + for infinite bounds u can just look at the function and take a good guess (x^5 -> inf will be divergent) e^-x from 0 to inf will go to 1 because
-e^0 = -1 (integral(e^-x) = -e^-x)
if u look at how e function goes u cna mirror it on y-axis and u see it goes to 0 for infinite, so F(inf) - F(0) = 0 - (-1) = 1
its what i know from high school tho maybe im dog now
probably some gay ass trigonometry (idk how, maybe turn cos/sin into tan), alternatively (what i would do, but probably wait for ALENOORI or someone else to answer) substitution
btw question for smarties, if lim f(x)_{x -> inf} = inf, does it mean that the function is always divergent, or is there an exception to this
The function is divergent if it does not converge to a real number. Infinity is not a real number, so f(x) does not converge in that case. There is no exception, at least for real valued functions.
But how do I derive (cos(x))/sin^2(x)
cosx/sin^2x = cotx*cscx
so for f(x) = cosx/sin^2x =cotx*cscx, f'(x) = cotx*(-cscxcotx) + cscx(-csc^2x) = -cscx(cot^2x+csc^2x)
it would suffice to leave it like that, thus the derivative of (cos(x))/sin^2(x) is -cscx(cot^2x+csc^2x).
Please try to avoid the quotient rule if possible. It just makes it messy and an unnecessary effort when you can utilize the trig identities to make your work easier.
Well for all intents and purposes, particularly in your case, there is no exception.
But if you ever take an analysis course, specifically complex analysis you will find that the complex plane and be extended so that it can be topologically equivalent, or homeomorphic to the riemann sphere. This is done by defining the notion of the complex infinity which allows us to have a different interpretation from the metaphorical infinity you will be working with in calculus.
In other words, infinity becomes a point in the set . It is important to note that this element is NOT a number is used to discuss limiting behavior of complex functions (for example those holomorphic at infinity).
But in the context of your calc class, the important part to understand is infinity is NOT a number but rather a metaphor used to distinguish between situations where points on a line become unbounded by getting large positively and negatively very fast.
If you choose to further pursue courses in analysis or maybe take the advanced calc sequence it would still be favorable to understand how this notion of infinity can have different interpretations depending on the structure you are studying.
i am fairly sure that you don't need some cosmic shit like csc to solve that
too bad that i forgot how to do calculus so i can't back up my statement by solving it normally
If you do not have a solid grasp of being able to use identities to manipulate trig functions to compute derivates, let alone not even know what csc and cot are, you are going to struggle horribly in calc 1, and you will fail calc 2, and be just like all of those other people I see complaining about it being too difficult without actually taking the time to do the problems or read the text and proceeding to drop every class they get a C in on the first exam.
So for his sake he better hope he does not consider the equality cosx/sin^2x = cotxcscx as "cosmic shit" because that is the easiest braindead solution to a simple trig derivative like that. Any other solution (ie the suggestion to use the quotient rule) is just more work than is needed and shows that the person making the suggestion lacks profeciency with the tools he should be familiar with at this point in the course.
Edit: I know it sounds harsh but if I am correct in assuming you (ywn) are in calc 1 then you really should have a good grasp on the foundations of trig functions and their associated identities. Especially when you get to calc 2 you will be required to know almost all of the important ones like the back of your hand as it will benefit you greatly when you start doing more complicated trig integrals. If I was teaching your calc 1 class and you told me you never learned about cot and csc I would be very worried about what else you might have never learned and how this could impact your performance in this course.
and playing pos5 right now is literally the worst it has ever been. the games are so fucking unfun to play. i used to actually enjoy playing support but now i do it because no one else in their right mind wants to do it
well only one i cant do is e cause i dunno hwo to derive that shit
maths are hard and i've no clue how they are useful in life
basic skills is the other story, still can't figure our why limits and integral garbage are so important
im not going through that ever again
alenari men i thought u were gud
chain and product rule probably is very important for u to learn,
integral(e^-x) is -e^-x
only way to solve this is by what triple said, F(b) - F(a) + for infinite bounds u can just look at the function and take a good guess (x^5 -> inf will be divergent) e^-x from 0 to inf will go to 1 because
-e^0 = -1 (integral(e^-x) = -e^-x)
if u look at how e function goes u cna mirror it on y-axis and u see it goes to 0 for infinite, so F(inf) - F(0) = 0 - (-1) = 1
its what i know from high school tho maybe im dog now
integral(f(x)) is probably false wording, i mean the main function (idk how its called in english), the F(x) for f(x)
btw question for smarties, if lim f(x) x -> inf is inf, does it mean that the function is always divergent, or is there an exception to this
Yes, if it is an inderterminant form for this case one. No exception if the value of limit tends to inf.
But how do I derive (cos(x))/sin^2(x)
It is U/V form it's derivation is [(dU/dx)V - (dV/dx)U]/V^2
Other method is u convert it into cot(x).cosec(x)
Apply U.V form [(dU/dx).V+(dV/dx)U]
Your welcome.
Ye but I never learned about cot and cosec
And i tried the first one but I couldn't get it right gg
probably some gay ass trigonometry (idk how, maybe turn cos/sin into tan), alternatively (what i would do, but probably wait for ALENOORI or someone else to answer) substitution
oh nvm mister darth already got it :) seems overkill tho
But I can't do it cuz I'm bad
just learn it lol 4head dont u have places where u practice this in class
sym why u leave discord n delete me)
The function is divergent if it does not converge to a real number. Infinity is not a real number, so f(x) does not converge in that case. There is no exception, at least for real valued functions.
cosx/sin^2x = cotx*cscx
so for f(x) = cosx/sin^2x =cotx*cscx, f'(x) = cotx*(-cscxcotx) + cscx(-csc^2x) = -cscx(cot^2x+csc^2x)
it would suffice to leave it like that, thus the derivative of (cos(x))/sin^2(x) is -cscx(cot^2x+csc^2x).
Please try to avoid the quotient rule if possible. It just makes it messy and an unnecessary effort when you can utilize the trig identities to make your work easier.
are there exceptions with non real valued functions
Well for all intents and purposes, particularly in your case, there is no exception.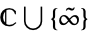 . It is important to note that this element is NOT a number is used to discuss limiting behavior of complex functions (for example those holomorphic at infinity).
. It is important to note that this element is NOT a number is used to discuss limiting behavior of complex functions (for example those holomorphic at infinity).
But if you ever take an analysis course, specifically complex analysis you will find that the complex plane and be extended so that it can be topologically equivalent, or homeomorphic to the riemann sphere. This is done by defining the notion of the complex infinity which allows us to have a different interpretation from the metaphorical infinity you will be working with in calculus.
In other words, infinity becomes a point in the set
But in the context of your calc class, the important part to understand is infinity is NOT a number but rather a metaphor used to distinguish between situations where points on a line become unbounded by getting large positively and negatively very fast.
If you choose to further pursue courses in analysis or maybe take the advanced calc sequence it would still be favorable to understand how this notion of infinity can have different interpretations depending on the structure you are studying.
now thats some pogchamp stuff
i am fairly sure that you don't need some cosmic shit like csc to solve that
too bad that i forgot how to do calculus so i can't back up my statement by solving it normally
If you do not have a solid grasp of being able to use identities to manipulate trig functions to compute derivates, let alone not even know what csc and cot are, you are going to struggle horribly in calc 1, and you will fail calc 2, and be just like all of those other people I see complaining about it being too difficult without actually taking the time to do the problems or read the text and proceeding to drop every class they get a C in on the first exam.
So for his sake he better hope he does not consider the equality cosx/sin^2x = cotxcscx as "cosmic shit" because that is the easiest braindead solution to a simple trig derivative like that. Any other solution (ie the suggestion to use the quotient rule) is just more work than is needed and shows that the person making the suggestion lacks profeciency with the tools he should be familiar with at this point in the course.
Edit: I know it sounds harsh but if I am correct in assuming you (ywn) are in calc 1 then you really should have a good grasp on the foundations of trig functions and their associated identities. Especially when you get to calc 2 you will be required to know almost all of the important ones like the back of your hand as it will benefit you greatly when you start doing more complicated trig integrals. If I was teaching your calc 1 class and you told me you never learned about cot and csc I would be very worried about what else you might have never learned and how this could impact your performance in this course.
studying LUL just go to work
Well I just started and didn't learn that cot/csc stuff in hs so. Also this is not NA
wat is this math cancer that i will not understand unless i put effort
Anyway thanks for help I can prob do it now
ywn 9k at dota 1k at math
i actually got the right stuff using the quotient rule it seems, i just had problems simplyfying it
Rip dondo
symetrical i got a minor gift for u, hope u see it on time
https://epulze.com/dota2/tournaments/2017
region restriction - UK only
bump
Nigga we made it
?
fuck the haters triple u get me?
no
played 5 games, grimstroke won every single one. totally balanced hero nothing wrong
and playing pos5 right now is literally the worst it has ever been. the games are so fucking unfun to play. i used to actually enjoy playing support but now i do it because no one else in their right mind wants to do it
sam the beta male
so grimstroke is still broken even after nerfs?
"nerfs"
okay i actually give up
How to grimstroke
you just pick it. the enemy will automatically concede the game
have a classic
i don't think i've won a single game with grimstroke regardless on which team he is
What even were the nerfs
That hero is insane but i see a lot of people losing with it for no reason